ニュートン法は方程式を数値計算によって解くアルゴリズムです。
\(f(x) = 0\) における解を求めることができます。
具体的には以下の漸化式を繰り返し計算していき、十分に収束すればその時のxを解とします。
\(x_{n+1}=x_n-\frac{f(x_n)}{f^\prime(x_n)}\)
今回は2つの方法を紹介します。
scipy.optimize.newton()- ニュートン法の実装
scipy.optimize.newton()
scipy.optimize.newton(func, x0)
func : f(x)=0におけるf(x)x0 : xの初期値fprime : funcの微分(ドキュメントによると、fprimeを与えるとニュートン法が使われるが、与えなければセカント法が使われるらしい)
\(\sqrt{3}\)を求めてみたいと思います。
\(\sqrt{3}\)を求める方程式は\(x^2-3=0\)です。
from scipy.optimize import newton
def f(x):
return x**2 -3
def fp(x):
return 2*x
print(newton(f, 4, fprime=fp))
# 1.7320508075688774勘が良い方はお気づきかもしれませんが、\(x^2-3=0\)の解は\(\sqrt{3}\)だけでなく\(-\sqrt{3}\)も含まれます。
算出される解はxの初期値に依存するので、初期値を変更すると\(-\sqrt{3}\)が算出されます。
from scipy.optimize import newton
def f(x):
return x**2 -3
def fp(x):
return 2*x
print(newton(f, -0.5, fprime=fp))
# -1.7320508075688772scipy.optimize.newton — SciPy v1.12.0 Manual
ニュートン法の実装
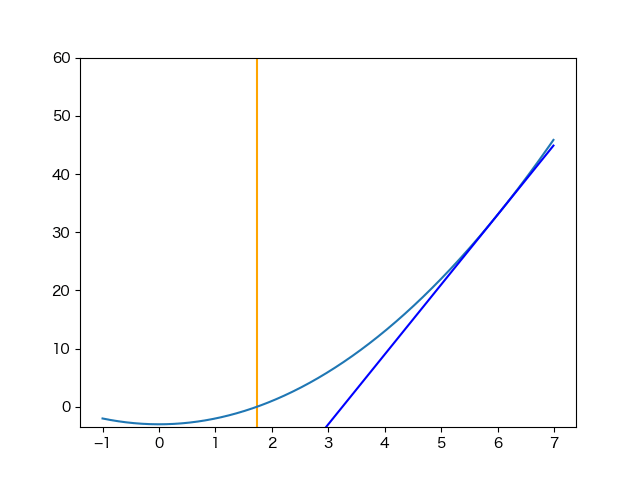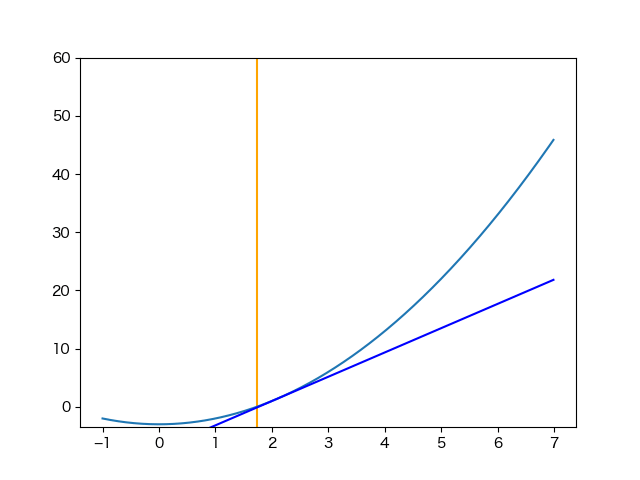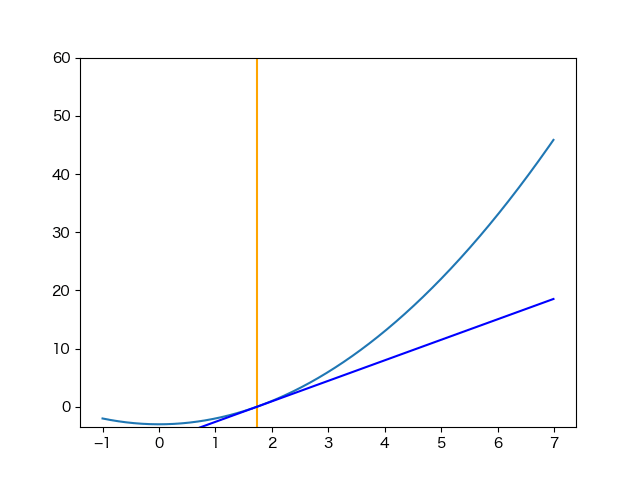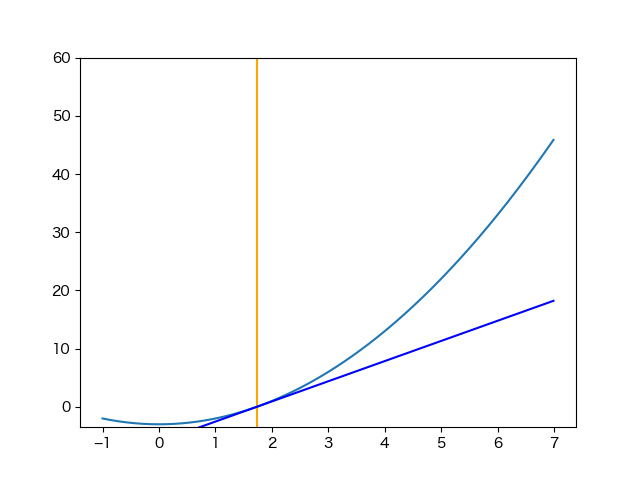
ライブラリで用意されているのであまり実装する機会はないと思いますが、簡単なのでニュートン法を実装してみました。
この記事の冒頭に書いた漸化式をコードにしただけですが…
def newton(func, fprime, x0):
x = x0
while True:
x = x - func(x)/fprime(x)
if abs(f(x) - 0) < 0.0000001:
return x
def f(x):
return x**2-3
def fprime(x):
return 2*x
print(newton(f, fprime, 6))
# 1.7320508266751493
print(newton(f, fprime, -6))
# -1.7320508266751493アニメーションのコードはこちらです。
拙いコードですが、役立てていただければ…
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation
def newton(func, fprime, x0):
x = x0
xs = [x0]
while True:
x = x - func(x)/fprime(x)
xs.append(x)
if abs(f(x) - 0) < 0.0000001:
return xs
def f(x):
return x**2-3
def fprime(x):
return 2*x
xlim_left = -1
xlim_right = 7
ylim_bottom = -3.5
ylim_top = 60
x = np.arange(xlim_left, xlim_right, 0.01)
newton_xs = newton(f, fprime, 6)
fig = plt.figure()
plt.ylim(ylim_bottom, ylim_top)
plt.plot(x, f(x))
plt.vlines(np.sqrt(3), ylim_bottom, ylim_top, color='orange')
# フレームの作成
frames = []
for newton_x in newton_xs:
y = fprime(newton_x)*x + f(newton_x)-fprime(newton_x)*newton_x
frame = plt.plot(x, y, color='blue')
frames.append(frame)
# 描画
ani = ArtistAnimation(fig, frames, interval=1000)
# 保存
ani.save('newton_method.gif')




コメント